Существуют математические и графические методы расчета лестниц. Математические методы довольно объемны и сложны, поэтому графические методы чаще всего применяются на практике. Наиболее распространенными из графических методов являются метод пропорций и метод разверток. Все они дают примерно равные результаты по прокладке ступеней.
О расчете забежных ступеней методом пропорций мы рассказывали в другой статье, ознакомиться с ней вы можете, перейдя по ссылке. В данной статье рассмотрим метод разверток.
Метод разверток
Опишем процесс расчета лестницы с поворотом 900 с забежными ступенями.
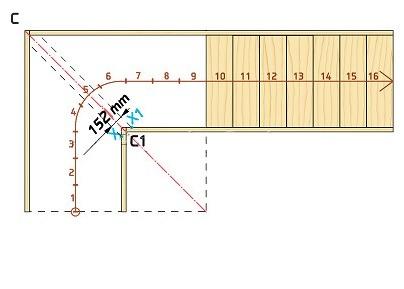
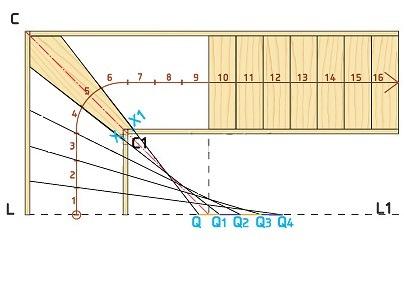
- Необходимо начертить две пары параллельных линий, расположенных перпендикулярно друг к другу. Расстояние между параллельными линиями должно быть равно ширине марша лестничного пролета.
- Затем необходимо отметить толщину тетивы или косоура.
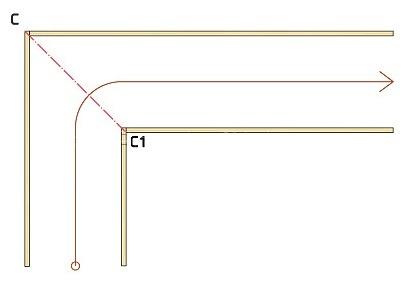
- Далее построим среднюю линию и проведем ось C — C1.
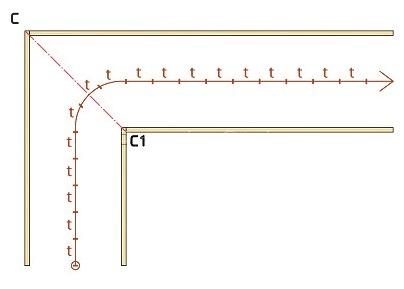
- Теперь на средней линии необходимо отметить ширину ступеней.
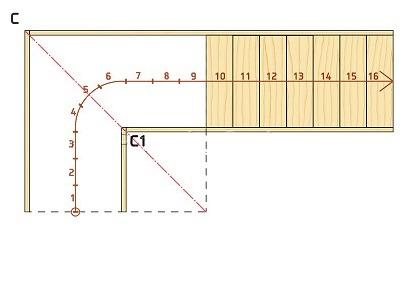
- Мы определяем необходимое количество забежных ступеней в повороте. В нашем случае у нас будет 9 поворотных ступеней. Определив последнюю прямую ступень в каждом марше, проводим от них линии до тех пор, пока они не пересекутся с осью C — C1.
- Теперь проведем линии, параллельные оси C-C1, на расстоянии 76 мм в каждом направлении. В совокупности мы получим значение 152 мм, которое составляет минимальный размер проступи.
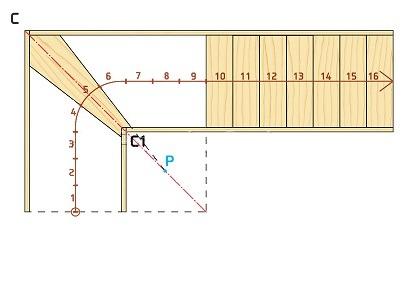
- Отметим точку Р, которая равна середине отрезка от С1 до точки пересечения продленных линий последних прямых ступеней. Проведя линии Р-X и Р-X1 до внешней тетивы (косоура), получим центральную поворотную ступень.
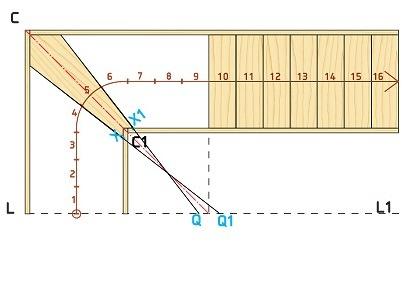
- Теперь мы продолжим обе стороны центральной ступени, пока они не пересекут ось L — L1. В результате мы получим отрезок Q-Q1 на оси L — L1.
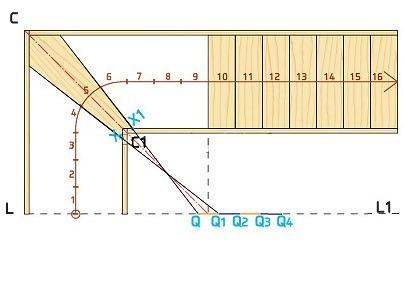
- Справа от отрезка Q-Q1 необходимо повторить на один отрезок меньше необходимого количества ступеней до центральной ступени, в нашем случае 3 отрезка.
- Соединив точки отрезков с отметками ширины ступеней, получим форму поворотных ступеней, расположенных с одной стороны центральной ступени.
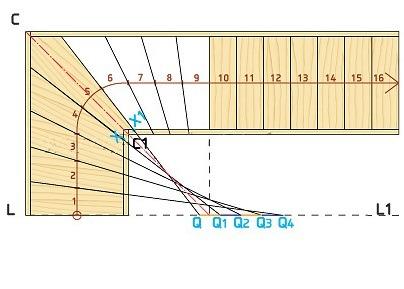
- Чтобы получить форму поворотных ступеней, расположенных на другой стороне от центральной части, необходимо повторить все действия п. 8-10 симметрично относительно оси C-C1.
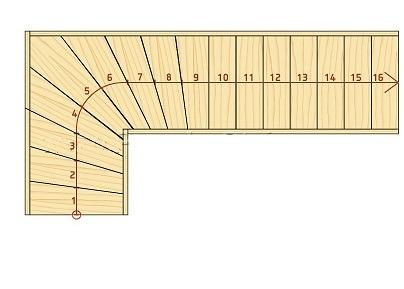
- В результате получим поворотную лестницу с забежными ступенями, рассчитанными по методу разверток.